Issue 2 Article 4

The Hardy-Weinberg Principle and how to break its Equilibrium

25/2/20

By:

Lee Zhe Yu, Nathan

Edited:

Elijah Chew Ze Feng

Tag:

Study Buddies

In 1908, an English mathematician named Godfrey H. Hardy and a German physician named Wilhelm Weinberg independently worked out a mathematical relationship between the frequency of genotypes and the alleles that conferred said genotypes. This groundbreaking revelation, taking on the surnames of its discoverers, quickly became an integral part of inheritance studies. Today, the Hardy-Weinberg Principle is still prevalent in population genetics, and also the A-level Biology Paper. In fact, the Hardy-Weinberg Principle has been added to the H2 Biology Syllabus 9477 for students taking the A-levels from 2026 onwards. This article unpacks the workings of the Hardy-Weinberg Principle and how it can be applied in your exams.

Introduction

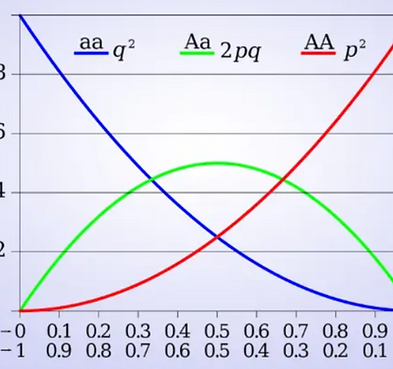
To visualise the Hardy-Weinberg Principle, let's start off with a population of fish. The colour of each of these fish is determined by a gene with two alleles: p and q. All of the fish have two copies of the allele, hence there must be a total of (population size * 2) alleles. Each of the alleles must either be a p or a q allele, hence:

no. of p alleles + no. of q alleles = population size * 2 = total no. of alleles

Since each fish has two alleles of the gene, the potential genotypes are homozygous p (pp), heterozygous (pq), or homozygous q (qq). In the population, homozygous p fish are red, heterozygous fish are purple, and homozygous q fish are blue. Hence:

no. of pp individuals + no. of pq individuals + no. of qq individuals = population size

However, the Hardy-Weinberg Principle is used to measure allelic frequencies. This involves probability. Since the chances of an allele being an allele is always the case by definition, the variable (total no. of alleles) is equal to 1. The allelic frequencies of each of the alleles can be obtained by taking the number of alleles of that type over the total number of alleles. By letting p be the frequency of the p allele in the fish population, and q be the frequency of the q allele in the population:

∴ p + q = 1

This equation is one of the two main equations of the Hardy-Weinberg Principle.

Quadratic Equations

To derive the second main equation of the Hardy-Weinberg Principle, we will have to go back to a previous equation. The genotypic frequency of each genotype can be traced back to the frequency of its combination of alleles. Hence, the probability of the homozygous p and homozygous q genotypes are as follows:

To calculate the genotypic frequency of the heterozygous genotype, we must take into account the possibility of the order of the alleles. Since the genotype is independent of the order of the alleles, we would need to multiply by 2 when calculating the heterozygous genotypic frequency:

Since all organisms must have a genotype, the (population size) variable in equation 2 can likewise be replaced by 1. In addition, the genotypic frequency of each genotype is also the number of organisms with that genotype over the total population size. Hence:

pp genotypic frequency + pq genotypic frequency + qq genotypic frequency = population size

This results in the following equation:

As you might have already realised, this is basically just the square of the first main Hardy-Weinberg equation mentioned earlier (p + q = 1):

This can be explained by the fact that all alleles result in one of the three possible genotypes, and since each genotype is a multiplication between the allelic frequencies of its constituent alleles, taking the square of the allelic frequency equation would result in the genotypic frequency equation.

Extension

This principle works with any number of alleles. The three-allele version is shown below:

Let p, q, r, be the allelic frequencies of the three alleles:

The Hardy-Weinberg Principle is also inherently linked to probability, where the frequency of each genotype / allele can also refer to the probability that by selecting one random organism / allele, it would be of the desired genotype / allele type.

Back to Reality

A population that fulfills the Hardy-Weinberg Principle is said to be in Hardy-Weinberg Equilibrium. In the above example, the fish population (2 pp fish, 4 pq fish and 2 qq fish) does fulfil this requirement (p = 0.5; q = 0.5). Unfortunately, few, if any, populations achieve this equilibrium in the real world, mostly due to five assumptions it heavily relies on.

Assumption #1: No mutations

Mutations involve an allele changing from one type to another. Since mutations change allelic frequencies, a mutation would affect the expected genotypic frequencies through the Hardy-Weinberg and actual genotypic frequencies, causing them to no longer be the same. If a mutation introduces a new allele into the population, the population would not have had time to adjust to this change, disturbing Hardy-Weinberg Equilibrium as well.

Assumption #2: Large Population Size

This condition is largely dependent on a phenomenon called genetic drift. Since mating and inheritance is inherently probabilistic, there might be variations in genotype frequency and allelic frequency, disturbing Hardy-Weinberg Equilibrium. While in large populations, these fluctuations are usually minor, in smaller populations, alleles can become fixated (i.e. completely dominant), leading to the loss of the variant allele.

Assumption #3: No Migration

Migration, along with mutation, changes the allelic and genotypic frequencies to differing extents, resulting in a mismatch between the expected genotypic frequencies from Hardy-Weinberg Equilibrium and the observed genotypic frequencies in the population. When caused by migration, this phenomenon is known as gene flow.

Assumption #4: Random Mating

This assumes that all organisms are given equal chance to mate with each other in order to pass on their alleles. To maintain population numbers, each organism is assumed to produce two children, with each of their two alleles being passed on to exactly one offspring. If some organisms are preferably mated with, their alleles would be likely to pass on their alleles to more offspring, resulting in changes in allelic and genotypic frequency that disrupt Hardy-Weinberg Equilibrium once again.

Assumption #5: No evolution

This assumes that no genotype has a selective advantage / disadvantage over the others. If there is a disparity in terms of its ability to survive or reproduce, the genotype would be selected for / against by natural selection. This would tend to increase / decrease the numbers of organisms with that genotype, depending on the severity of its increased / decreased ability. The end result is that Hardy-Weinberg Equilibrium is disrupted.

A-Level Biology Crash Course

We will now go through some potential exam questions regarding the Hardy-Weinberg Equilibrium. (Do note that due to the new syllabus change, there has not been any questions set in past year A levels as well as prelim papers)

Case #1 (H2 Biology Syllabus 9477 Specimen Paper 1 Q25)

Within populations, there can be large amounts of genetic variation, leading to a range of different phenotypes for some characteristics (polymorphisms). For example, shell pattern in the snail Cepaea nemoralis is under genetic control and is highly polymorphic. Shells can be yellow, pink or brown with a range of different banding patterns. Which condition would maintain the polymorphism, in a population, of a characteristic that is under genetic control?

A. preferential mating with individuals having recessive phenotypes

B. occurrence of a natural disaster in which only a few, randomly selected individuals of a large population survive

C. consistent selection pressure against characteristics controlled by dominant alleles

D. population being in Hardy–Weinberg equilibrium

Answer: D

Hardy-Weinberg Equilibrium tends to maintain allelic frequencies, allowing for polymorphism to continue to be expressed in the population.

Options A and C result in a selective advantage for recessive genotypes, causing dominant alleles to eventually reduce in frequencies to zero and phenotypes involving the expression of those dominant alleles to decrease in number to zero, reducing polymorphism. Option B is an example of the “bottleneck event” whereby the population size is drastically reduced. This causes drastic changes in allelic frequencies, and can cause alleles to be lost in the new population, reducing polymorphism.

Case #2

In Singapore, 1 in 10000 people is born with sickle cell disease, an autosomal recessive disease. The Singapore population is assumed to be in Hardy-Weinberg equilibrium.

a) Calculate the frequency of the recessive allele.

b) Determine the percentage of Singaporeans who are carriers.

Answers:

References

Issue 7 - July 2025

The Hardy-Weinberg Principle and how to break its Equilibrium